Details
library(ggplot2); theme_set(theme_bw(base_size = 15))
library(data.table)First, some data
Details
dat <- data.table(
x = gl(2, 10, 20),
z = gl(2, 5, 20))
X <- model.matrix( ~ . * ., data = dat)
beta <- c(1, 2, 3, 1)
dat$y <- rnorm(20, X %*% beta, 1)Plot the data:
Details
## calculate means by each group
means <- dat[, .(m = mean(y)), by = .(x, z)]
## plot means with raw data
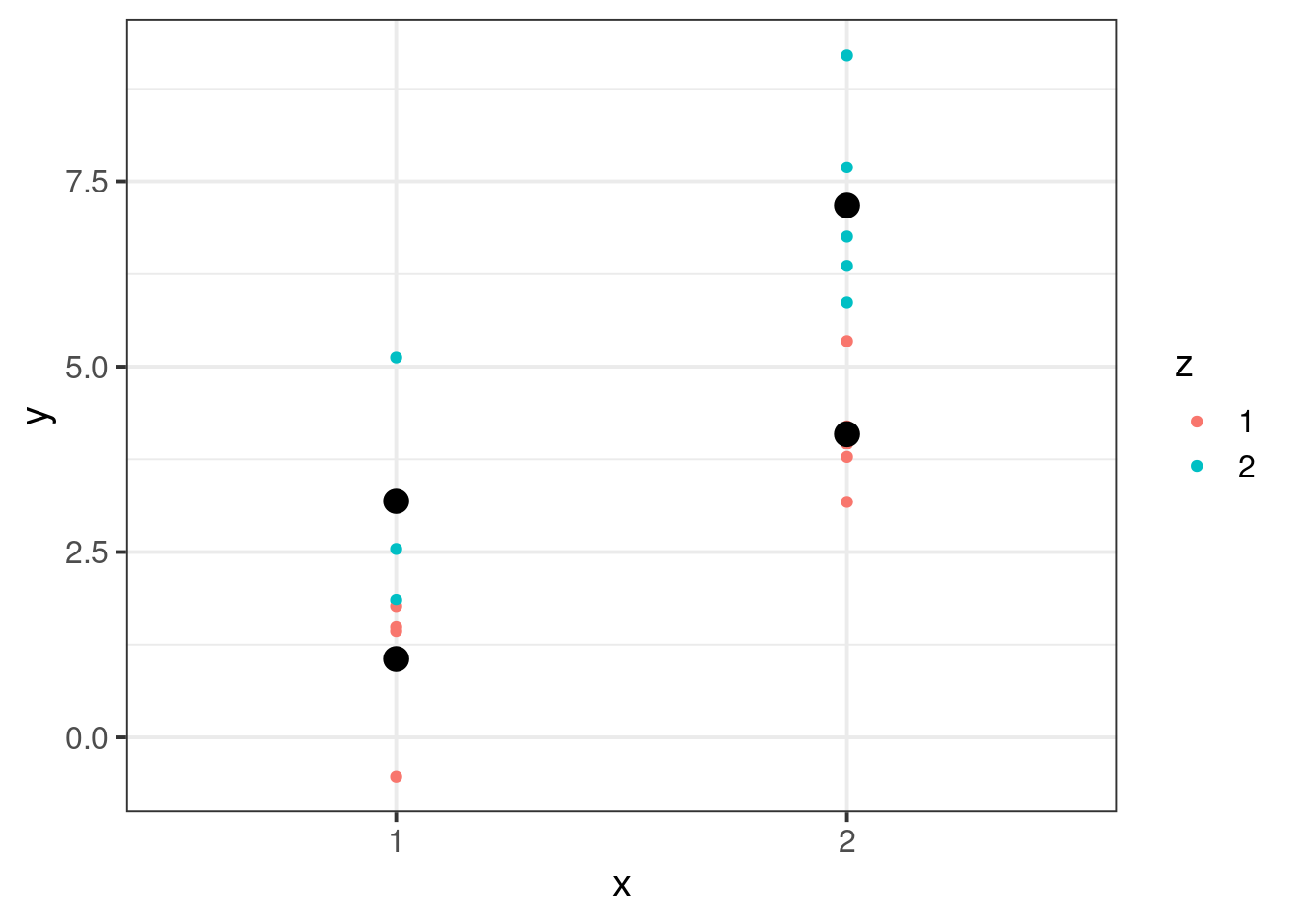
p <- ggplot(dat, aes(x = x, y = y, color = z, group = interaction(x, z))) +
geom_point() +
geom_point(data = means, aes(y = m), fill = 'black', col = "black", size = 4, shape = 21)
pWhen we fit an ANOVA model, what do the coefficients mean? We can interpret them geometrically. Below, I will plot the betas visually, to show how they sum to give the group means. There is no unique way to do this, so I will just show some of the two more common versions.
The way that group means decompose to parameters in the ANOVA model is called a contrast coding.
Treatment Coding
First we set the data for plotting:
Details
fit_treat <- lm(y ~ . * ., data = dat)
coefs <- coef(fit_treat)
smat <- unique(X)
sm <- unique(dat[, c("x", "z")])
for (j in 1 : ncol(X)) {
set(sm, j = paste0("beta", j - 1), value = as.matrix(smat[, 1 : j]) %*% coefs[1 : j])
}
out <- melt(sm,
id.vars = c("x", "z"),
measure.vars = patterns("beta"),
variable.name = "Coefficient",
value.name = "yend")
out[, ystart := shift(yend, type = "lag"), by = .(x, z)]
out[is.na(out)] <- 0Then render the plot:
Details
p2 <- ggplot(means, aes(x = x)) +
ggtitle("Treatment Coding") +
xlab("x") +
ylab("y") +
geom_segment(data = out,
aes(x = x, xend = x, y = ystart, yend = yend,
color = Coefficient), size = 2) +
geom_point(aes(y = m),
fill = 'black', col = "black", size = 4, shape = 21) +
ylim(c(0, NA))
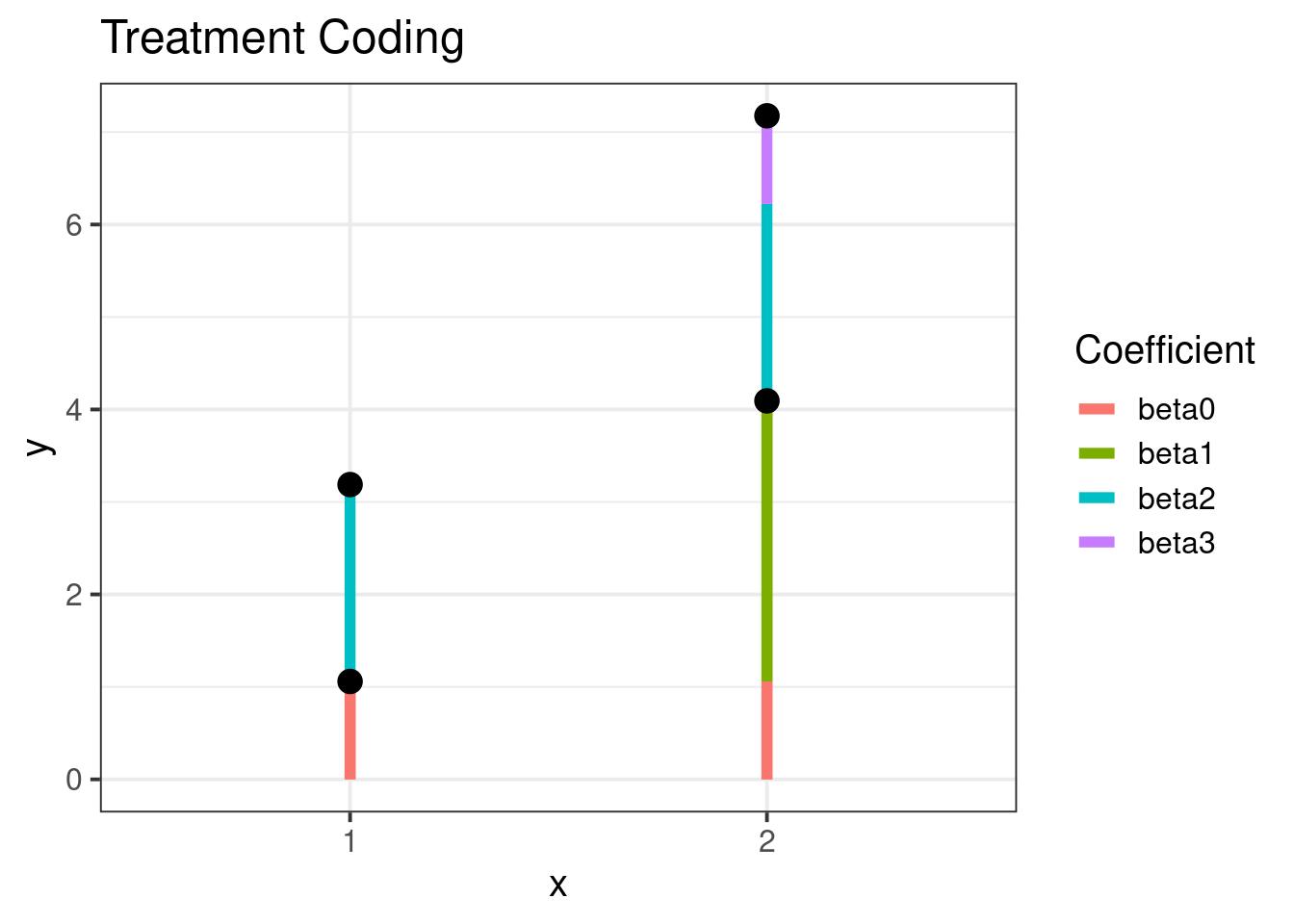
p2The plot shows the following treatment code relation visually:
| x level | z level | ANOVA Estimate |
|---|---|---|
| Low | Low | |
| Low | High | |
| High | Low | |
| High | High | + + + |
Sum-to-Zero Coding
With Sum coding, it will look a little different.
Details
fit_sum <- lm(y ~ . * ., data = dat,
contrasts = list("x" = "contr.sum",
"z" = "contr.sum"))
coefs <- coef(fit_sum)
X2 <- model.matrix( ~ x * z, data = dat,
contrasts.arg = list("x" = "contr.sum",
"z" = "contr.sum"))
smat <- unique(X2)
sm <- unique(dat[, c("x", "z")])
for (j in 1 : ncol(X)) {
set(sm, j = paste0("beta", j - 1), value = as.matrix(smat[, 1 : j]) %*% coefs[1 : j])
}
out2 <- melt(sm,
id.vars = c("x", "z"),
measure.vars = patterns("beta"),
variable.name = "Coefficient",
value.name = "yend")
out2[, ystart := shift(yend, type = "lag"), by = .(x, z)]
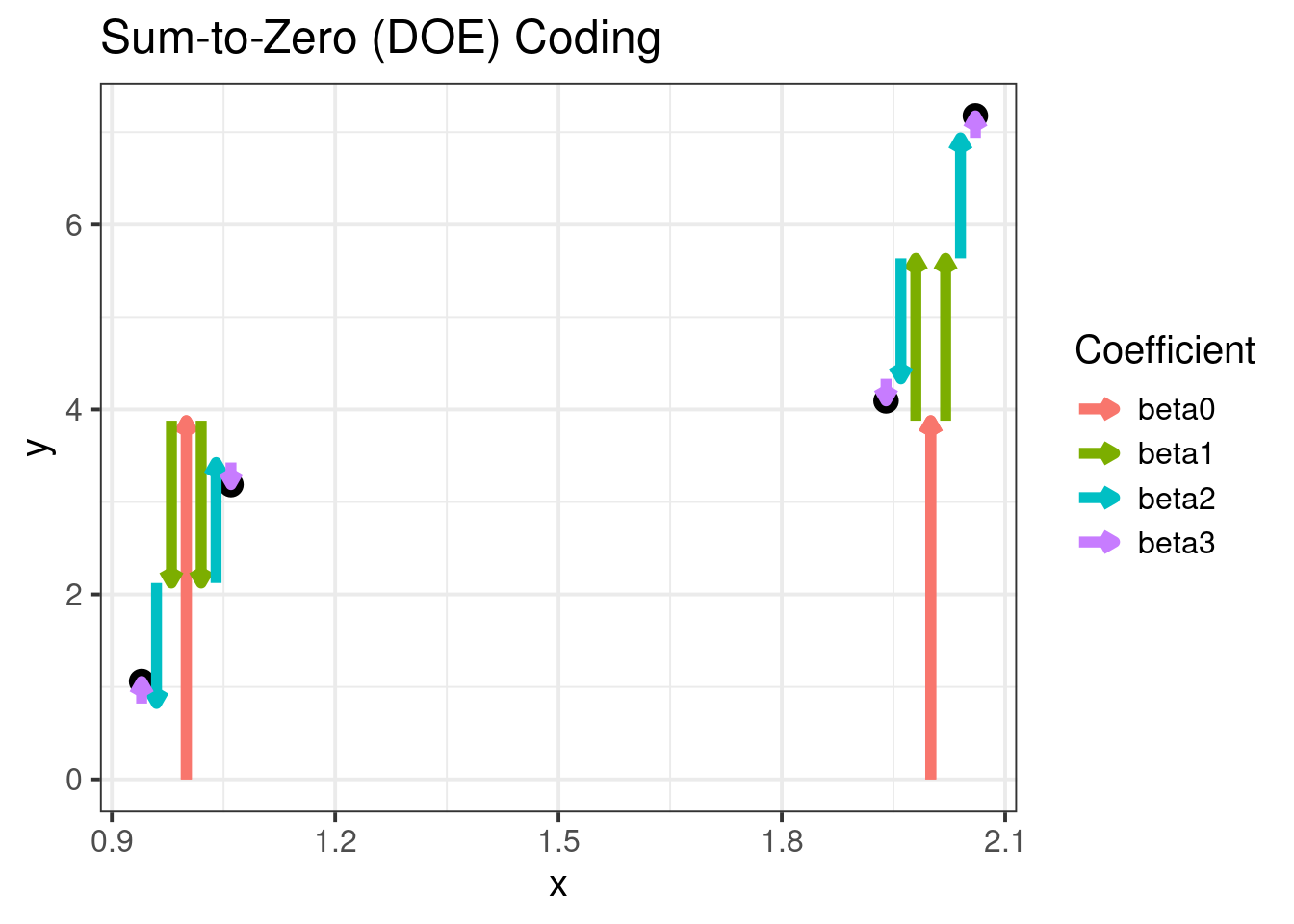
out2[is.na(out2)] <- 0In this case, we need to jitter the x-values to show how the coefficients sum to give the group means:
Details
xj <- c(0, 0, 0, 0,
-0.02, 0.02, -0.02, 0.02,
-0.04, 0.04, -0.04, 0.04,
-0.06, 0.06, -0.06, 0.06)Then render the plot:
Details
p3 <- ggplot(means, aes(x = as.numeric(x) + xj[13 : 16],
y = m)) +
ggtitle("Sum-to-Zero (DOE) Coding") +
xlab("x") +
ylab("y") +
geom_point(aes(y = m),
fill = 'black',
col = "black",
size = 4,
shape = 21) +
geom_segment(data = out2,
aes(x = as.numeric(x) + xj,
xend = as.numeric(x) + xj,
y = ystart,
yend = yend,
color = Coefficient),
arrow = arrow(length = unit(0.2, "cm")),
size = 2) +
ylim(c(0, NA))
p3The plot shows the following DOE coding relation visually:
| x level | z level | ANOVA Estimate |
|---|---|---|
| Low | Low | - - + |
| Low | High | - + - |
| High | Low | + - - |
| High | High | + + + |