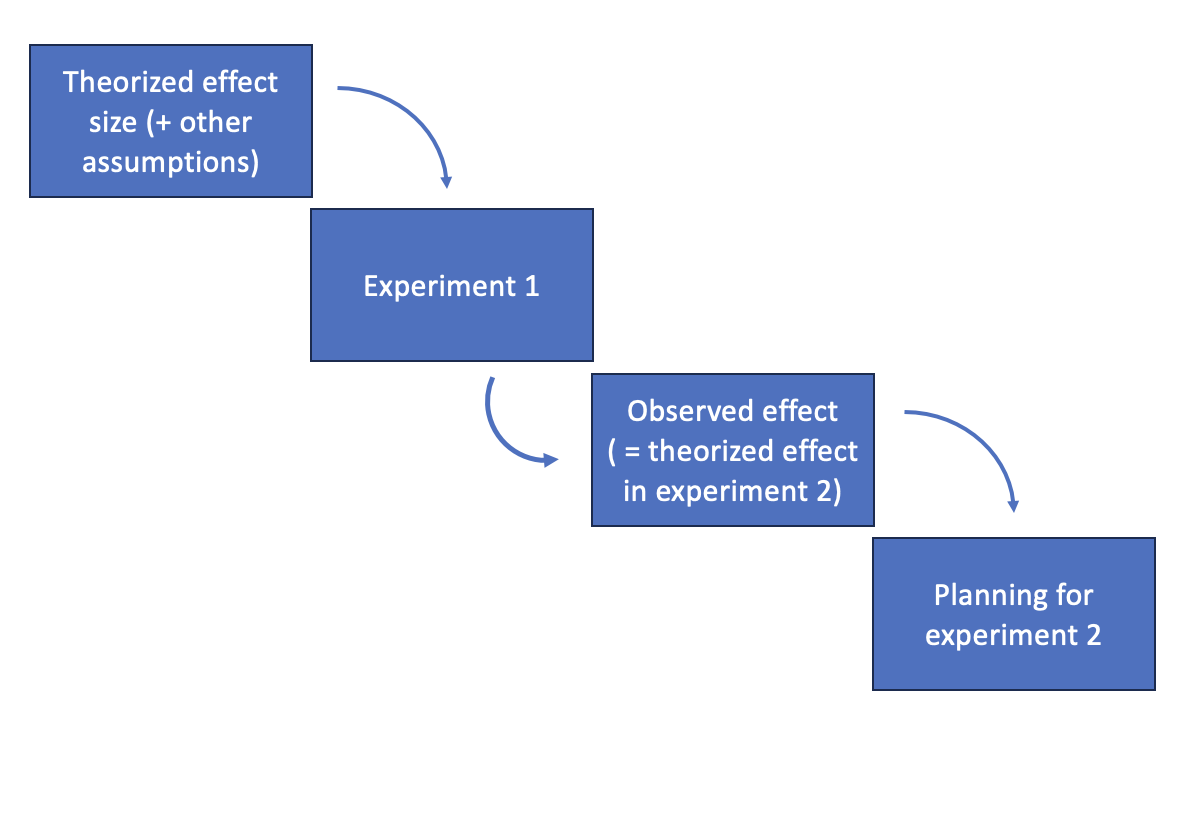
Here is a problem I’ve seen a few times: Suppose we propose a design for a test of a system. The experimental design is based on power analysis, so we select and execute the design that is 80% power for some kind of effect we want to observe.
We conduct the test, get the data, and get some estimates of the effect size.
What do we do with this information when we design the next test of a similar system? A natural thing to do is take the observed effect (aka signal to noise ratio) and plug it into the next power analysis as the theoretical effect.
However, taking the observed effect as the theorized effect has some problems. If the observed effect is small, this means that the next study will be planned with a larger number of trials. If the observed effect is large, the next study will be smaller. If the effect size is big, then the statisticians might have an easy job.
Yet, with a small observed effect, some project managers will complain: “We already did some testing on a similar system. This means we learned something, and we don’t have to do so much testing in the future. Why do we have to do more data collection now?” This can be a tricky area for statisticians performing power analyses, and it’s going to require a careful explanation for the project manager.
In my view, this is where power analysis can provide some bad incentives and outcomes if blindly applied, and it’s good rationale for multiple design selection criteria in experimental design. A natural question, is “what is the best we can do with the effect sizes from prior analyses”.
I don’t think there is a simple answer: statisticians need to be careful when using this prior study information in a power analysis. Statisticians also must think carefully about the purpose of the power analysis – is the research goal of the study really what is being studied in the power analysis? Often, in my work, the answer is “no”.
So, here are some tips for planning a study that is going to be similar to a previous one.
Ensure that the power analysis is really aimed at the goal of the study. Just because you can justify a sample size with a power analysis, doesn’t mean any power analysis will do the job!
Work across the spectrum of stakeholders (both statisticians and non-statisticians) to make sure the planners are all using the prior information in a consistent way.
Consider metrics other than power that are more amenable to prior information use. For example, reduction in entropy or margin of error. Or use methods from sequential experimentation. Many experiments are more about effect characterization than small p-values.
Work with all stakeholders to ensure that everyone understands how the new system is expected to differ from the old system.
I’m afraid that I don’t have a simple answer for this one, but it is a problem that I hope to study later. I imagine there are many good solutions, and maybe a flowchart could be used to determine best path forward for follow-on studies.